01. 릴레이션 분해란?
릴레이션 분해는 하나의 릴레이션을 두 개 이상의 릴레이션으로 나누는 것입니다. 릴레이션을 분해하면 중복이 감소되고 갱신 이상이 줄어드는 장점이 있는 반면에, 바람직하지 않은 문제들을 포함하여 몇 가지 잠재적인 문제들을 야기할 수 있습니다.
첫째, 일부 질의들의 수행 시간이 길어집니다. 릴레이션이 분해되기 전에는 조인이 필요 없는 질의가 분해 후에는 조인을 필요로 하는 질의로 바뀔 수 있습니다. 둘째, 분해된 릴레이션들을 사용하여 원래 릴레이션을 재구성하지 못할 수 있습니다. 셋째, 어떤 종속성을 검사하기 위해서는 분해된 릴레이션들의 조인이 필요할 수 있습니다. 따라서 이런 잠재적인 문제와 중복성 감소 간의 균형을 고려해야 합니다.
다음의 학생 릴레이션은 함수적 종속성들이 만족됩니다.
[학생] 릴레이션
| 학번 | 이름 | 이메일 | 과목번호 | 학점 |
| 11002 | 이홍근 | sea@hanmail.net | CS310 | A0 |
| 11002 | 이홍근 | sea@hanmail.net | CS313 | B+ |
| 24036 | 김순미 | smkim@naver.com | CS345 | B0 |
| 24036 | 김순미 | smkim@naver.com | CS310 | A+ |
학번 → 이름, 이메일
이메일 → 학번, 이름
(학번, 과목 번호) → 학점
한 학생이 여러 과목을 수강한다면 이 학생의 투플들에서 (학번, 이름, 이메일)이 중복해서 나타나 갱신 이상이 발생할 수 있습니다. 정보의 중복을 해결하기 위해 학생 릴레이션을 두 개의 릴레이션 학생 1과 수강으로 분해해볼 수 있습니다. 두 릴레이션으로부터 학생 릴레이션을 다시 얻으려면 자연 조인을 수행합니다. 학생 1 릴레이션과 수강 릴레이션에서 학번은 기본 키와 외래 키 관계이므로 두 릴레이션을 조인하면 원래의 학생 릴레이션에 들어 있는 정보를 완전하게 얻을 수 있습니다. 이런 분해를 무손실 분해(lossless decomposition)라 합니다. 여기서 손실은 투플의 손실이 아니라 정보의 손실을 의미합니다. 정보의 손실은 원래의 릴레이션을 분해한 후에 생성된 릴레이션들을 조인한 결과에 들어 있는 정보가 원래의 릴레이션에 들어있는 정보보다 적거나 많은 것을 모두 포함합니다.
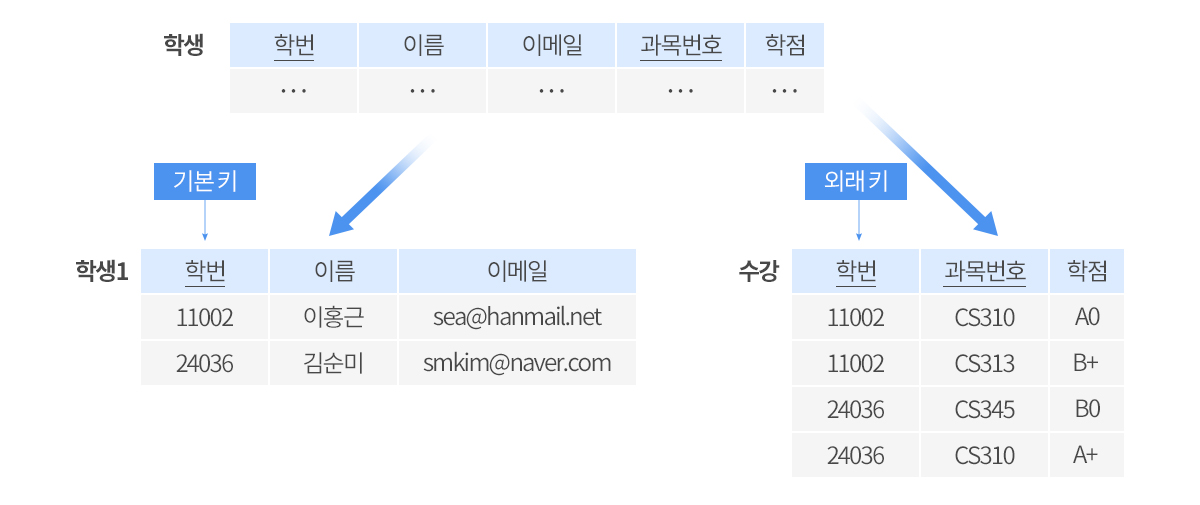
학생 1 릴레이션을 그림 7.10처럼 또다시 분해하는 것은 불필요합니다. 학생 1 릴레이션의 기본 키는 학번이고 이름과 이메일이 한 번에 직접 함수적으로 종속하므로 학생 1 릴레이션을 추가로 분해하면 학번만 불필요하게 두 번 저장됩니다. 또한 학생 1 릴레이션에는 불필요한 중복이 존재하지도 않습니다.

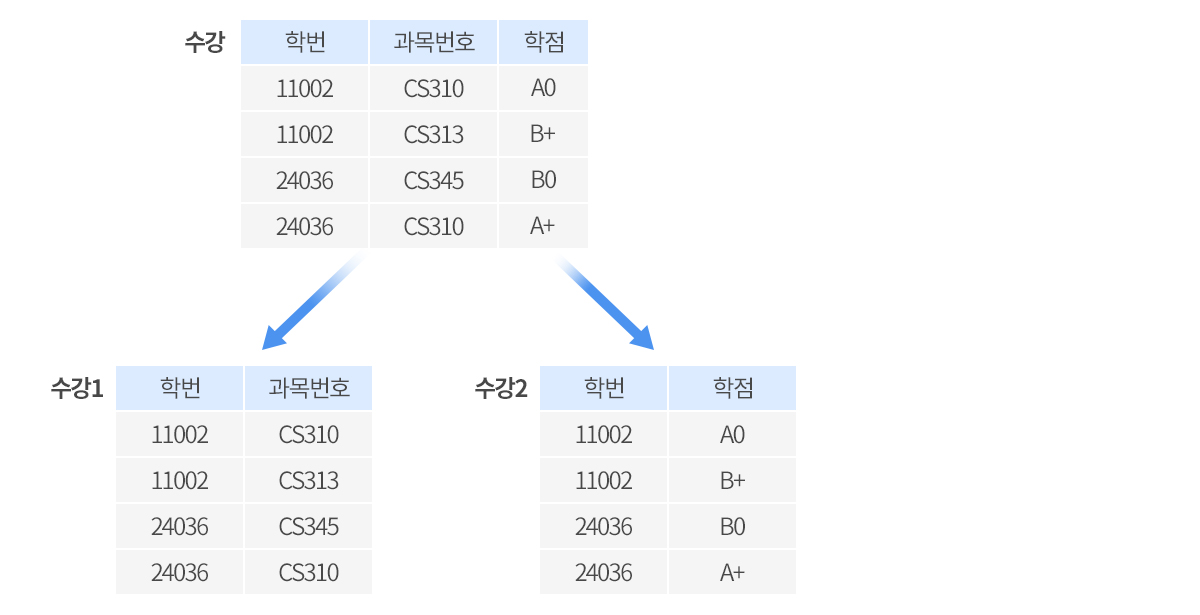
수강 릴레이션을 그림 7.11처럼 분해하면 과목 번호와 학점 간의 연관이 표현되지 않으므로 나쁜 분해입니다. 또한 수강 1과 수강 2 릴레이션을 조인하면 수강 릴레이션에 들어 있는 투플보단 많은 투플이 생성됩니다. 따라서 이 분해는 무손실 분해가 아닙니다. 수강 릴레이션에 없는 투플이 수강 1과 수강 릴레이션의 조인 결과에 생긴 것을 가짜 투플(spurious tuple)이라고 말합니다.
02. 제1정규형, 제2정규형, 제3정규형, BCNF
정규형에는 제1정규형, 제2정규형, 제3정규형, BCNF, 제4정규형, 제5정규형 등이 있지만 일반적으로 데이터베이스를 설계할 때 3NF 또는 BCNF까지만 고려합니다. 제2정규형부터는 BCNF까지의 정규형은 함수적 종속성 이론에 기반을 둡니다.
▶︎ 제1정규형
한 릴레이션 R이 제1정규형을 만족할 필요충분조건은 릴레이션 R의 모든 애트리뷰트가 원자값만을 갖는다는 것입니다. 즉 릴레이션의 모든 애트리뷰트에 반복 그룹(repeating group)이 나타나지 않으면 제1 정규형을 만족합니다. 반복 그룹은 한 개의 기본 키값에 대해 두 개 이상의 값을 가질 수 있는 애트리뷰트를 의미합니다.
| 학번 | 이름 | 과목번호 | 주소 |
| 11002 | 이홍근 | { CS310 , CS313 } | 우이동 |
| 24036 | 김순미 | { CS310 , CS345 } | 양재동 |
[그림 7.13] 반복 그룹
제1정규형을 만족하지 않는 그림 7.13을 제1정규형을 변환하는 한 가지 방법은 반복 그룹 애트리뷰트에 나타나는 집합에 속한 값마다 하나의 투플입니다. 그림 7.14는 이런 방법을 적용하여 그림 7.13을 제1정규형을 만족하는 릴레이션으로 변환한 예를 보여줍니다. 그림 7.14의 제1정규형은 정보가 많이 중복되므로 7.1절에서 설명한 바와 같이 갱신 이상을 유발합니다.
| 학번 | 이름 | 과목번호 | 주소 |
| 11002 | 이홍근 | CS310 | 우이동 |
| 11002 | 이홍근 | CS313 | 우이동 |
| 24036 | 김순미 | CS345 | 양재동 |
| 24036 | 김순미 | CS310 | 양재동 |
[그림 7.14] 애트리뷰트에 원자값만 있는 릴레이션
제1정규형을 만족하지 않는 그림 7.13을 제1정규형으로 변환하는 또 다른 방법은 모든 반복 그룹 애트리뷰트들을 분리해서 새로운 릴레이션에 넣습니다. 원래 릴레이션의 기본 키를 새로운 릴레이션에 애트리뷰트로 추가합니다. 원래 릴레이션의 기본 키가 새로운 릴레이션에서도 항상 키가 되는 것은 아닙니다. 그림 7.15는 이런 방법을 적용하여 그림 7.13을 제1정규형을 만족하는 릴레이션으로 변환한 예를 보여줍니다.
'💕IT 공부하기 > 데이터베이스' 카테고리의 다른 글
| 함수적 종속성에 대해 알고계신가요? (0) | 2022.09.16 |
|---|---|
| 릴레이션 정규화에 대해서 (0) | 2022.09.15 |
| 물리적 데이터베이스 설계에 대하여(5) (0) | 2022.09.14 |
| 물리적 데이터베이스 설계에 대하여(4) (0) | 2022.09.13 |
| 물리적 데이터베이스 설계에 대하여(3) (0) | 2022.09.12 |